Vertaling en analyse van woorden door kunstmatige intelligentie ChatGPT
Op deze pagina kunt u een gedetailleerde analyse krijgen van een woord of zin, geproduceerd met behulp van de beste kunstmatige intelligentietechnologie tot nu toe:
- hoe het woord wordt gebruikt
- gebruiksfrequentie
- het wordt vaker gebruikt in mondelinge of schriftelijke toespraken
- opties voor woordvertaling
- Gebruiksvoorbeelden (meerdere zinnen met vertaling)
- etymologie
Wat (wie) is Мера множества - definitie
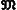 - некоторое семейство его подмножеств. Неотрицательную функцию μ(A), определённую для всех А, входящих в
- некоторое семейство его подмножеств. Неотрицательную функцию μ(A), определённую для всех А, входящих в  , называют мерой, если она вполне аддитивна [т. е., если для любой последовательности непересекающихся множеств A1, A2,..., An,..., входящих в
, называют мерой, если она вполне аддитивна [т. е., если для любой последовательности непересекающихся множеств A1, A2,..., An,..., входящих в  , сумма А которых входит в
, сумма А которых входит в  , имеет место равенство
, имеет место равенство удовлетворяет определённым дополнительным условиям. Множества, входящие в
удовлетворяет определённым дополнительным условиям. Множества, входящие в  , называют измеримыми (по отношению к мере μ). После того как определена мера μ, вводят понятие измеримых (по отношению к μ) функций и операцию интегрирования.
, называют измеримыми (по отношению к мере μ). После того как определена мера μ, вводят понятие измеримых (по отношению к μ) функций и операцию интегрирования.Wikipedia
Ме́ра мно́жества — числовая характеристика множества, интуитивно её можно понимать как массу множества при некотором распределении массы по пространству. Понятие меры множества возникло в теории функций вещественной переменной при развитии понятия интеграла.
Собственно, мера — это некоторая числовая функция, ставящая в соответствие каждому множеству (из некоторого семейства множеств) некоторое неотрицательное число. Кроме неотрицательности мера как функция должна также обладать свойством аддитивности — мера объединения непересекающихся множеств должна равняться сумме их мер. Необходимо отметить, что не всякое множество измеримо — для каждой функции меры обычно подразумевается некоторое семейство множеств (называемых измеримыми по данной мере), для которых мера существует.
Частным случаем меры является мера Лебега для подмножеств , обобщающая понятие объёма , площади или длины на случай множеств, более общих, чем просто ограниченные гладкой поверхностью.
